
|
NOTA:
Este libro se vende con un pequeño billar a escala, con un elástico para la práctica de los bricoles. EL LIBRO ESTÁ MUY BIEN EXPLICADO Y CREO QUE CON LA AYUDA DEL BILLAR MONITOR PODEMOS APRENDER FACÍLMENTE LA TEORÍA DEL SISTEMA DE DIAMANTES. |

| En este libro se hallan condensados los conocimientos necesarios para poder desarrollar el juego de Tres Bandas mediante el sistema de diamantes. | |
CONTIENE: | |
|
1.- Prólogo
2.- Introducción 3.- Numeración y Llegadas 6.- Bricoles por tres bandas 10.- Prácticas sobre el Monitor 12.- Carambolas por tres bandas 16.- Llegadas y bricoles por cuatro y cinco bandas 21.- Carambolas por cuatro y cinco bandas 24.- Aplicación de conocimientos 27.- Compensaciones |
|
| INTRODUCCION |
| El juego del Billar, que ya se practicaba como pasatiempo en la época de Luis XV, ha ido evolucionando poco a poco hasta convertirse en nuestra siglo en uno de los deportes más apasionantes y más complejos.
Son muy pocos los aficionados que, jugando por intuición, puedan conseguir buenos promedios. Los grandes jugadores de hoy en día, ayudados por la técnica de la teoría de los diamantes, han logrado alcanzar la tranquilidad y seguridad en su juego, la fortaleza necesaria que les permite ejecutar con bastante perfección, las carambolas y bricoles de tres, cuatro a cinco bandas. La teoría que vamos a estudiar, creada por Roger Conti, se basa principalmente en dar a las bandas una numeración adecuada y efectuar unos sencillos cálculos que nos permitirán conocer con toda exactitud el recorrido de la bola del jugador. Debo mencionar que muchos aficionados que trataron de aprender esta teoría tuvieron dificultades en memorizar las numeraciones de las bandas, lo cual les indujo a cometer errores de cálculo, debidos principalmente a la falta de práctica del sistema. Por tal motivo, he creado el Billar Monitor (*) que permite practicar y memorizar las numeraciones con suma facilidad. |
(*) El Billar Monitor es un billar pequeñito a escala, con un elástico para la práctica de los bricoles. |
| CAPITULO 2 | |
| Para ejecutar correctamente las jugadas por el sistema de diamantes, colocaremos el taco en posición horizontal y jugaremos con máximo efecto favorable. El golpe debe ser penetrado y con fuerza normal.
Usaremos siempre los rombos como punto de referencia, es decir, las líneas de salida-ataque y de llegada, serán tomadas siempre en la dirección de rombo a rombo. Los cálculos se efectuarán mediante la fórmula siguiente: Banda Llegada = Banda Salida - Banda Ataque Abreviando: LL = S-A Empezaremos a trabajar con el sistema tratando de resolver algunos problemas de bricoles por tres bandas. En la figura 3 tenemos un ejemplo: |
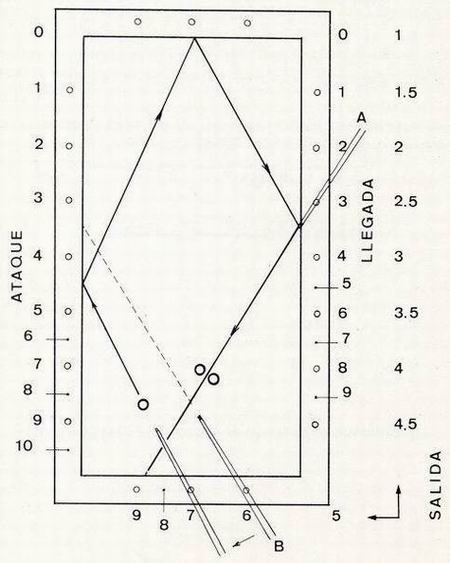
Figura 3 |
| Ante todo, es preciso conocer con exactitud el punto de llegada de tercera banda para hacer la carambola.
Nos serviremos del taco para verificar, en posición A, la dirección de ésta línea de llegada. Comprobamos que la llegada es 3, pues la línea va de 3 a 9. Entonces podemos colocar en la fórmula que: 3 = S - A. Como se puede apreciar, tenemos dos incógnitas por resolver, que son Salida y Ataque, las cuales a su vez están relacionadas con la bola del jugador y situadas en una línea recta que, partiendo de la banda de salida y pasando por el centro de la bola del jugador, incidirá sobre la banda de ataque. Esta es la parte más difícil del problema para el principiante pero, obrando con calma y serenidad, veremos que es de fácil solución. Efectuemos una resta que nos dé por resultado 3 desde uno de los rombos de la banda de salida. Supongamos que salimos del rombo 6 y que deseamos llegar al 3. Entonces diremos: 3 = 6 - 3. Coloquemos nuestro taco en posición B, es decir, salida 6, ataque 3. Esta línea no es la correcta, pues ya sabemos que debe pasar por el centro de la bola; por tanto, como nuestra bola está situada más a la izquierda, desplacemos paralelamente el taco hacia la bola y verifiquemos que la línea que pasa por el centro de ésta es la solución, pues se comprueba que: 3 = 7 - 4. Ahora podemos ejecutar el bricol con seguridad, atacando a 4. |
|
| Para irnos familiarizando con el sistema, trataremos de resolver el bricol de la figura 4.
En primer lugar debemos encontrar el punto de llegada de tercera banda. Colocando el taco en posición A, observamos que está en la línea 1 --> 10, que corresponde a la llegada 1. Este será el único dato conocido de la fórmula, pues los otros dos no los conocemos. Tomando como referencia uno de los rombos que esté situado más cerca de nuestra bola, efectuaremos una resta que dé 1 por resultado. En este caso, como hemos tomado como referencia el rombo 6, diremos: 1 = 6 - 5 Esta línea de salida 6-ataque 5 va, sin duda, hasta la llegada 1. Pero como sabemos que esta línea que buscamos, debe pasar necesariamente por el centro de nuestra bola, desplazaremos paralelamente el taco hasta encontrarla. Dejaremos el taco en esta posición y verificaremos de nuevo la resta. En el problema expuesto la línea buscada es salida 5 y ataque 4. Puesto que: 1 = 5 - 4 |
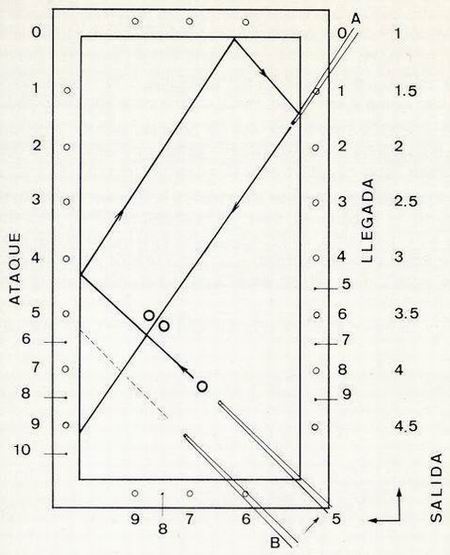 Figura 4 |
| Calculemos el bricol detallado en la figura 5.
Comprobando con el taco en posición A la línea de llegada se aprecia que no estamos en llegada 2 ni tampoco en 3 sino en la línea de 2,5. Por tanto: 2,5 = S - A. Tomando un rombo de referencia de la banda de salida, por ejemplo el rombo 4, y efectuando una resta cuyo resultado sea 2,5, encontramos el ataque en 1,5. Como sabemos que esta línea debe pasar por el centro de la bola del jugador desplazaremos el taco hacia la derecha hasta encontrar, salida 3,5 - ataque 1, que es en realidad la línea que buscamos, puesto que: 2,5 = 3,5 - 1. En infinidad de ocasiones nos encontraremos en la necesidad de efectuar sustracciones con números decimales, debido a que las bolas no se hallan situadas exactamente en la misma línea de los rombos. Citaremos dos ejemplos: |
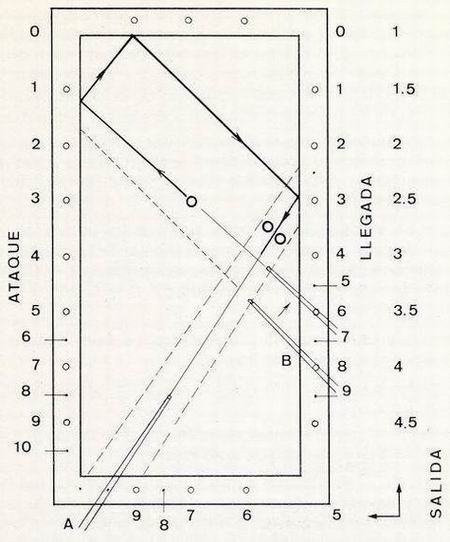 Figura 5 |
| CAPITULO 3 | |
| Al principio de este texto ya se mencionó que la mayor dificultad que encontraba el estudiante para la puesta en práctica del sistema, provenía, principalmente, de no disponer de un método didáctico apropiado para efectuar las prácticas de los conocimientos estudiados. Si trataba de desarrollar el sistema en una mesa de gran match debía necesariamente numerar las bandas mentalmente y efectuar una serie de cálculos que le producían una gran confusión al fin de los mismos y que, en la mayoría de los casos, le conducían a abandonar dicho sistema.
Creo sinceramente, que el Billar Monitor ayudará en gran manera a solventar tal problema y proporcionará al estudiante la oportunidad de efectuar las prácticas necesarias que han de permitirle familiarizarse con el uso de la teoría. |
|
|
Con el fin de obtener una mejor visual de los puntos de llegada se usa en este método la llegada de rombo a rombo.
|
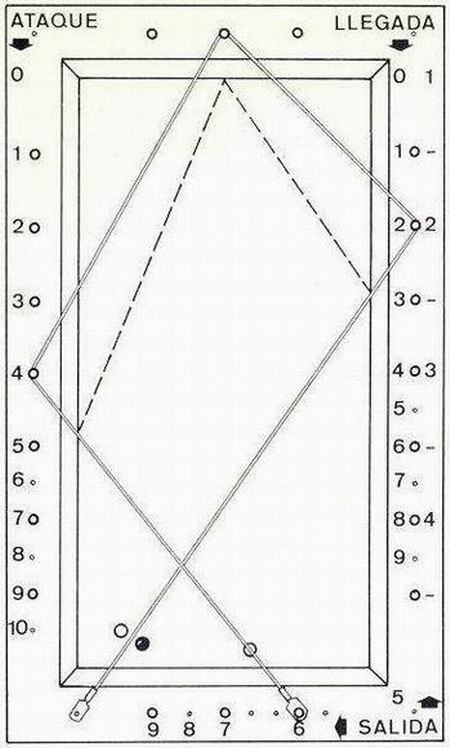 Billar Monitor |
| Como no se hace en el sistema un uso importante de la banda pequeña P, al llegar a ésta, se puede pasar el elástico por el rombo que se estime más conveniente. Debido a su fragilidad, se recomienda no tensar el elástico más allá de la cuarta banda.
Al efectuar las prácticas sobre el monitor consideraremos siempre la salida como un punto conocido. Así diremos: Si estamos en salida 4 y deseamos llegar a 3, tenemos que: 3 = 4 - 1. Nuestro ataque será 1. Si estamos en salida 8 y deseamos alcanzar la llegada 5 deberemos atacar en 3, puesto que: 5 = 8 - 3. Para adquirir un progreso rápido sobre el conocimiento del sistema, es imprescindible que el estudiante practique en el monitor, toda clase de bricoles y carambolas por tres bandas durante un período de varias semanas, emplazando siempre las bolas en sus respectivos lugares. Con ello, logrará retener en su mente la numeración de las bandas y las llegadas de tercera a cuarta banda, que son sin duda la base del sistema. Las carambolas y bricoles por cuatro y cinco bandas deben ser ensayados en una mesa de gran match, puesto que el monitor está diseñado especialmente para tres bandas. |
|
| CAPITULO 4 | |
| Vamos a tratar en este capítulo sobre el estudio de las carambolas por tres bandas, jugadas por medio del sistema de diamantes.
La diferencia que existe, en ejecutar un bricol o una carambola por tres bandas, radica, solamente, en la distinta situación de la línea salida-ataque respecto a la bola del jugador. Hemos visto que, en el bricol, la línea salida-ataque pasa también por el centro de la bola de jugador, sin embargo, en las carambolas por tres bandas diremos que esta línea salida-ataque es tangente a la bola contraria. Para una mayor claridad llamaremos bola 1 a la bola del jugador, bola 2 a la bola contraria y bola 3 a la bola que deseamos carambolear. La línea de llegada será la misma que hemos considerado para el bricol y, en este caso, pasará por el centro de la bola 3. Para efectuar nuestro cálculo se descartará totalmente a la bola 1, tratando de seguir el mismo orden metódico que hemos venido usando. |
|
| En la figura 7 se detalla un ejemplo de carambola por tres bandas.
En primer lugar, nos aseguraremos de la línea de llegada colocando el taco en posición A. Comprobamos que es la línea 4 --> 8, pues pasa precisamente por el centro de la bola 3. Seguidamente buscaremos la línea salida-ataque, cuya resta nos dé por resultado 4. Emplearemos el método que usamos en los bricoles, tratando, asimismo, que esta línea sea tangente a la bola 2. Se comprueba que la línea buscada es salida 6 --> ataque 2 pues: 4 = 6 - 2. Al ejecutar la jugada atacaremos la bola 1 (con efecto a la derecha) jugando sobre bola 2, tratando de alcanzar, con la mayor exactitud, el punto de ataque 2. La carambola de tres bandas se ha convertido, por así decirlo, en una carambola de bola 2 a ataque 2, que es realmente de fácil ejecución. "Toda carambola ejecutada por el sistema deberá ser atacada con el máximo efecto favorable si deseamos que cumpla los recorridos estudiados". |
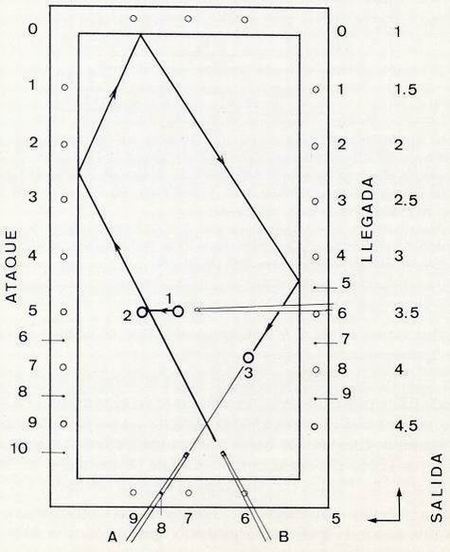 Figura 7 |
| Resolvamos la posición de carambola a tres bandas que se detalla en la figura 8.
Situemos nuestro taco en posición A para conocer la llegada requerida. Se comprueba que el punto de llegada es 1, pues la línea 1 --> 10 pasa por el centro de la bola 3. Busquemos ahora la línea salida-ataque, tangente a la bola 2, cuya diferencia sea 1. Efectuando los tanteos previos encontramos que: 1 = 2 - 1. Tenemos ya la solución del problema, pues sabemos que deberemos atacar en rombo 1. Jugaremos con máximo efecto a la derecha, tratando de tomar la cantidad de bola 2 suficiente e incidir sobre el ataque 1. Hecho lo cual, la carambola sale perfecta. Debemos recordar que el golpe debe ser penetrado y con el taco en posición horizontal. |
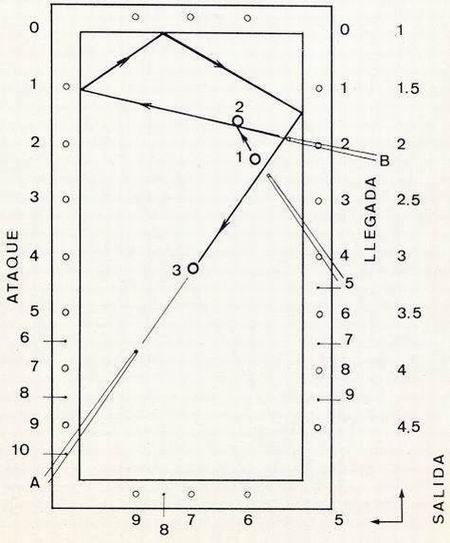 Figura 8 |
| Como punto final del capítulo, estudiemos la posición que se detalla en la fig. 9.
Verificamos que la llegada es 3, puesto que la bola 3 se halla situada en la línea de llegada 3 --> 9. Hallamos por el método que hemos usado en las ocasiones anteriores que la línea salida-ataque tangente a la bola 2, es, en efecto, la línea 7 --> 4, porque: 3 = 7 - 4. Deberemos atacar la bola 1 con máximo efecto a la derecha, tratando de tomar la cantidad de bola 2 suficiente para alcanzar el rombo de ataque 4. Creo conveniente, ahora, recomendar al estudiante el practicar sobre el Billar Monitor toda la gama posible de carambolas por tres bandas que, a no dudar, le permitirá asimilar sólidamente toda la materia estudiada. |
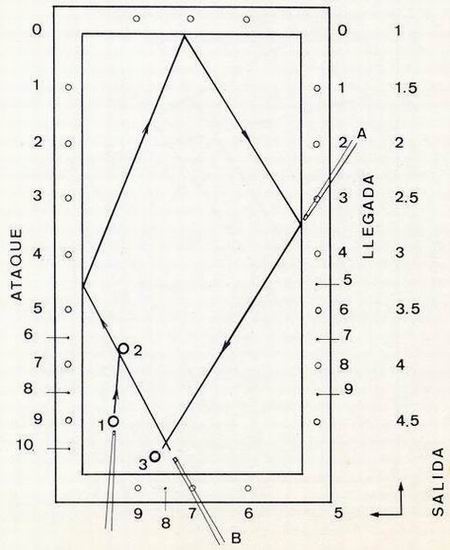 Figura 9 |
| Antes de entrar en el siguiente capítulo quisiera mencionar que el paño que cubre el billar debe ser de excelente calidad. Actualmente se usa en los campeonatos internacionales el paño super extra roulant "Iwan Simonis", el cual da excelentes resultados. Sin embargo, el rendimiento de las bandas difiere de un billar a otro, lo cual hace necesario efectuar unas pequeñas compensaciones que serán estudiadas al final de este libro. | |
| CAPITULO 5 | |
| Para entrar en el cálculo de los bricoles por cuatro y cinco bandas, será preciso conocer las llegadas de cuarta a quinta banda y de quinta a sexta banda.
En la figura 10 se detallan los recorridos de las mismas, en línea gruesa. Podemos apreciar que, si tomamos como centro el rincón E y trazamos unos arcos de circunferencia entre los puntos de llegada de la cuarta y quinta banda, se comprueba fácilmente que estas llegadas son equidistantes al rincón E. En lo que hace referencia a las llegadas de quinta a sexta banda se puede observar que éstas cumplen los mismos recorridos que las llegadas de tercera a cuarta banda, 3 --> 9, 2 --> R, 1 --> 10 y 0 --> 8, pero desplazadas en 3/4 de bola. Sin embargo, para facilitar al estudiante una mejor comprensión del tema, vamos a desestimar estos 3/4 de bola, efectuando los cálculos de los bricoles y carambolas por cinco bandas, suponiendo qué estas llegadas de quinta banda se corresponden exactamente con las llegadas de tercera banda. |
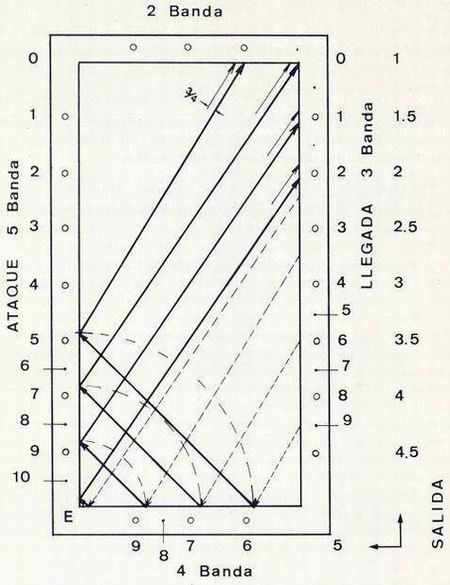 Figura 10 |
|
Como, a mi entender, estas nuevas llegadas serán asimiladas con facilidad por el estudiante vamos a proseguir nuestro estudio diciendo que para efectuar el cálculo se usará la llegada de tercera banda tal y como se ha venido haciendo hasta el presente.
Será necesario, por tanto, trasladar hacia atrás estas nuevas llegadas hasta hallar el punto de llegada de tercera banda. Para poner en práctica estos conocimientos trataremos de resolver el bricol por cuatro bandas que se observa en la figura 11. En primer lugar, deberemos hallar la línea de llegada de cuarta a quinta banda, para lo cual tomaremos como referencia los rombos de éstas (líneas de trazos) que son, sin duda, equidistantes al rincón. Colocando el taco, en posición A, encontramos por paralelaje el punto de llegada de la cuarta banda. Sin perder este punto de vista situaremos el taco en posición B para hallar la línea de llegada de tercera banda que coincide con el citado punto. Se observa que esta línea es la 3 - 9, que corresponde a la llegada 3. Ahora, sólo nos falta encontrar la línea salida-ataque, que pasando por el centro de la bola 1, nos dé una diferencia de 3; tenemos que: 3 = 7 - 4. Por tanto, jugaremos sobre ataque 4. |
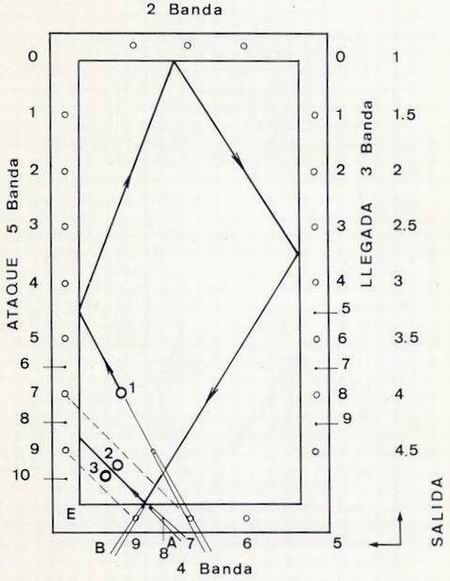 Figura 11. |
| Calculemos el bricol por cinco bandas de la figura 12.
Se tratará, en primer lugar, de encontrar el punto de llegada de quinta banda. Como se demostró que las llegadas de quinta banda siguen al mismo camino que las llegadas de tercera banda procuraremos hallar este punto de llegada como si se tratase de una llegada de tercera banda. Situaremos el taco en posición A, comprobando que estamos en linea de 3 --> 9. Sin perder de vista el punto de llegada de quinta banda colocaremos el taco en posición 8 para trasladar este punto de llegada a la cuarta banda. Con la referencia de los rombos equidistantes al rincón E encontraremos por paralelaje este punto. Por fin, situaremos el taco en posición C para determinar con exactitud la línea de llegada de tercera banda que incide en este punto. Se comprueba que esta línea es la 8 --> 6. Como que 8 es la llegada requerida, debemos encontrar la línea salida-ataque cuya resta sea 8, puesta que: 8 = 9 - 1. La solución es ataque 1. |
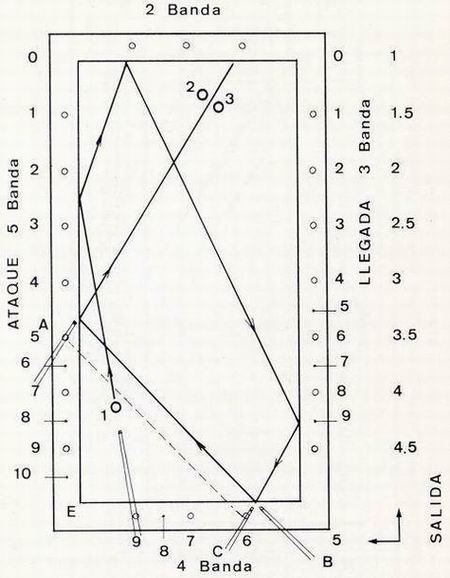 Figura 12 |
| En la figura 13 se observa otra posición de bricol por cinco bandas.
Siguiendo con nuestro método de trabajo, deberemos encontrar, primeramente, el punto de llegada de la quinta banda. Colocando el taco, en posición A, se observa que esta línea de llegada corresponde a la línea 2 --> Rincón. Situaremos el taco en posición B y trasladaremos, mediante el paralelaje entre rombos, esta llegada de quinta banda hacia la cuarta. Por último, colocaremos el taco en posición C para verificar la línea de llegada de tercera banda que incida sobre este punto de llegada de cuarta banda. Esta línea resulta ser la 5 --> 7, que corresponde a la llegada 5 de tercera banda. Aplicando la fórmula, encontramos que: 5 = 6,5 - 1,5. El ataque será 1,5. |
 Figura 13. |
| Como es de suponer que el estudiante habrá efectuado una gran cantidad de prácticas sobre el Monitor resolviendo bricoles y carambolas por tres bandas y que, sin duda, habrá memorizado la numeración de las bandas y las líneas de llegada de tercera banda, será necesario que comience a efectuar estas prácticas sobre un billar de gran match.
Es conveniente que en el local donde se efectúan las prácticas reine el mayor silencio, para obtener así una mayor concentración mental. Asimismo, deberá seguirse un orden metódico de trabajo, que ha de permitirnos, de una forma mecánica, llegar a la solución de todo problema. Cuando se ejecutan bricoles por cinco bandas y hay que dar un golpe fuerte, se deberá tomar en cuenta que se produce una cuadratura en el recorrido de la bola 1, pues los ángulos del recorrido tienden a cerrarse; por tal motivo, se tratara de dar un golpe penetrado y con mesura, haciéndose la debida compensación si fuese necesario. Debo mencionar, que los bricoles por cinco bandas expuestos en las figuras 12 y 13, deberán ser compensados en 3/4 de bola, es decir, "alargados". Asimismo, las carambolas de las figuras 15 y 16, también deberán ser compensadas de la misma forma, pues ya vimos con anterioridad que, las llegadas de quinta banda no coinciden exactamente con las llegadas de tercera banda. |
|
| CAPITULO 6 | |
| Para el estudio de las carambolas por cuatro y cinco bandas haremos uso de las llegadas de cuarta y quinta banda que han sido tratadas en e capítulo anterior, trasladando éstas hasta la tercera banda para efectuar el cálculo correspondiente.
Veamos el ejemplo de carambola por cuatro bandas, que se detalla en la figura 14. Se colocará el taco, en posición A, para hallar los puntos de llegada de cuarta y quinta banda, los cuales sabemos que son equidistantes al rincón E. Fijaremos nuestra atención sobre el punto de llegada de cuarta banda y situaremos el taco, en posición B, para verificar la línea de llegada de tercera banda que incide en dicho punto. Comprobamos que la llegada requerida es el rombo 4, pues corresponde a la línea 4 --> 8. En posición C, buscaremos la línea de salida-ataque, tangente a bola 2. Encontramos que: 4 = 4 - 0. Deberemos jugar sobre bola 2 tratando de alcanzar el rincón 0. |
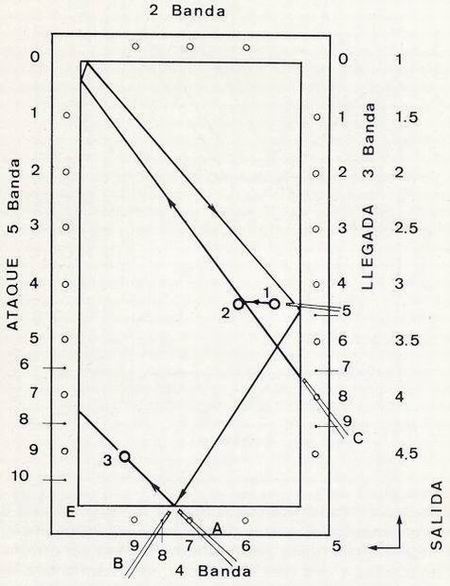 Figura 14 |
| Resolveremos la carambola por cinco bandas descrita en la figura 15.
En posición A, comprobamos la llegada de quinta banda que ha de permitirnos carambolear a la bola 3. Esta línea corresponde a 0 --> 8, y el punto de llegada está situado justamente a una bola del rincón. En posición B, emplazados a una bola del rincón, verificamos que la línea de llegada 2 -.> Rincón incide sobre este punto. Por tanto, nuestra llegada requerida de tercera banda, será 2. Finalmente, necesitamos buscar una línea salida-ataque, tangente a bola 2, cuya diferencia sea 2. En la posición C, hallamos esta línea, puesto que: 2=4,5-2,5. Jugaremos sobre bola 2 tratando de alcanzar el ataque 2,5. Al objeto de no confundir al estudiante con los cambios de numeración, he creído conveniente efectuar nuestro estudio emplazando la banda de ataque siempre a la izquierda del jugador. A partir de ahora, situaremos indistintamente esta banda a derecha o izquierda del mismo. |
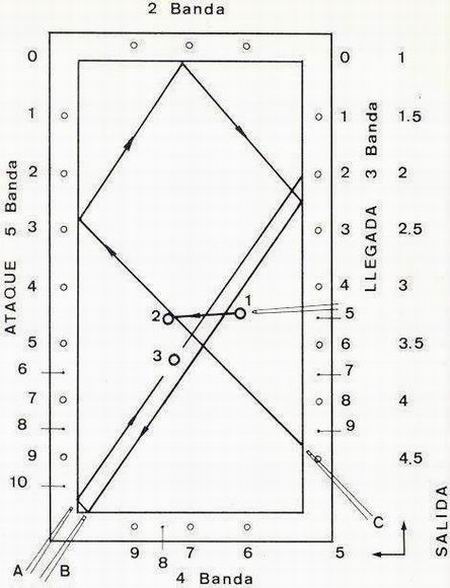 Figura 15 |
| Observemos otro ejemplo de carambola por cinco bandas, que se describe en la figura 16.
Colocando el taco, en posición A, comprobamos que la línea de llegada 3 --> 9 se corresponde con esta llegada de quinta banda. Obtenido este punto de llegada, nos situaremos, en posición B, para trasladar este punto a la cuarta banda por medio del paralelaje entre rombos equidistantes. Por último, en posición C, verificaremos que la línea de llegada de tercera banda coincida con el citado punto. Esta línea resulta ser la 8 --> 6, por tanto, nuestra llegada requerida será 8. En posición D, hallamos la línea salida-ataque, comprobando que: 8 = 9-1. |
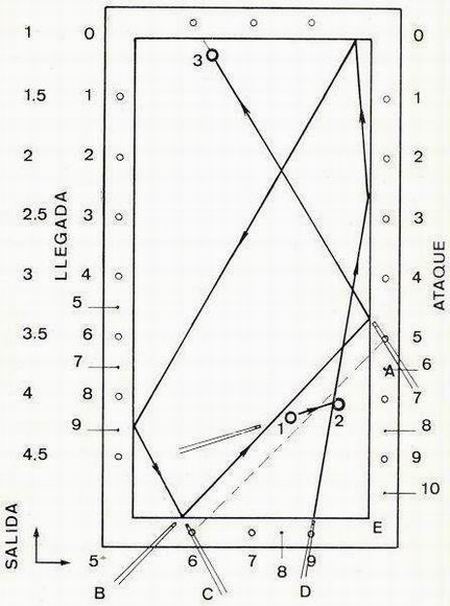 Figura 16 |
| CAPITULO 7 | |
| Si usamos racionalmente los conocimientos adquiridos y actuamos con una cierta lógica comprobaremos que somos capaces de resolver por teoría una amplia gama de posiciones que, a primera vista, parecen insolubles.
Como vía de ejemplo, me limitaré solamente a exponer tres posiciones, que han de permitir al jugador comprobar las muchas aplicaciones que puede tener el sistema. Tratemos de resolver la posición de la figura 17. Daremos a las bandas la numeración descrita y buscaremos la línea de llegada de tercera banda para carambolear la bola 3. Se comprueba, en posición A, que la línea de llegada es 2 --> Rincón, correspondiente a llegada 2. A continuación, nos situaremos en posición B para determinar la línea salida-ataque, cuya diferencia sea 2. Como estamos en salida 7, diremos que: 2 = 7 - 5. Jugaremos sobre la bola 2 con efecto favorable y golpe natural penetrado, tratando que nuestra bola, después de incidir sobre la banda pequeña, tome la línea de salida 7 --> 5. |
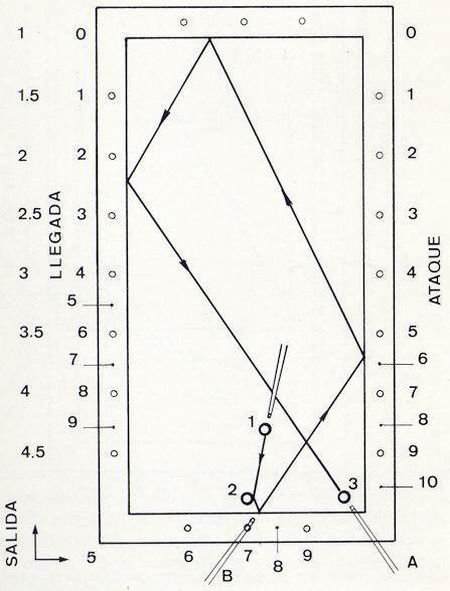 Figura 17 |
| En la figura 18 tenemos una posición de pasebola.
Comenzaremos buscando la línea de llegada, que ha de carambolear a la bola 3. En posición A, se comprueba que es 3,5. Seguidamente, nos coloraremos en posición B, sobre un punto tal que, jugando pasebola por la bola 2, sea fácil de alcanzar. En nuestro caso, verificamos que: 3,5 = 6,25 - 2,75, por tanto, la línea salida 6,25 ataque 2,75, será la solución. |
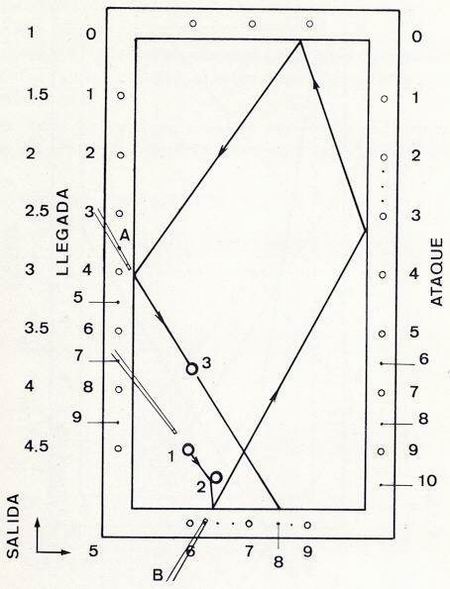 Figura 18 |
| Tratemos de resolver la difícil posición que se observa en la figura 19.
No es recomendable jugar un bricol por cinco bandas debido a que la bola 1 se halla situada demasiado cerca de la banda. Sin embargo, si estudiamos el problema por partes, podemos encontrar una solución más fácil. Vamos a suponer que el punto de salida se halla situado en la banda pequeña, por tanto, necesitaremos determinar el punto de llegada de tercera banda. Se observa en posición A que la llegada es 3. Nos colocaremos seguidamente en posición B, tratando de escoger un punto de salida, que nos permite alcanzar la línea salida-ataque deseada. En el problema hemos escogido el rombo de salida 6; aplicando la fórmula, encontramos que 3 = 6-3, es decir, salida 6 y ataque 3, será nuestra línea. Para ejecutar este tipo de jugadas con una cierta garantía, será imprescindible practicarlas, al objeto de saber escoger con una cierta lógica, la línea salida-ataque requerida. |
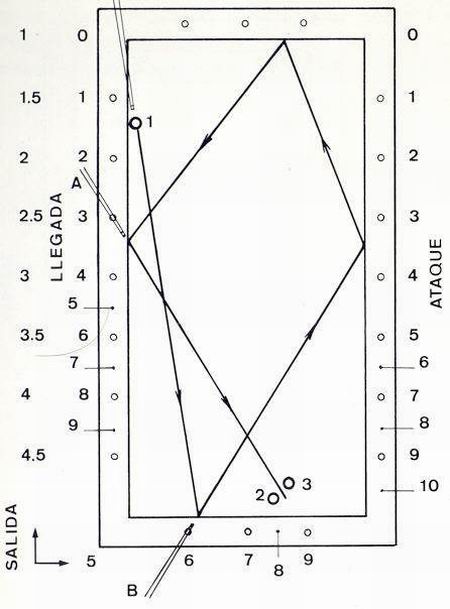 Figura 19 |
| COMPENSACIONES | |
| Antes de empezar un match, es preciso conocer de antemano el rendimiento de las bandas.
Ya hemos mencionado que estos rendimientos difieren de un billar a otro, estando relacionados con la calidad del material y, quizás en mayor grado, con la climatización del local. Las corrientes de aire y la humedad, son factores negativos, que inciden en el buen rendimiento de una mesa de billar. Será necesario, por tanto, efectuar unas pruebas previas y verificar desde distintos puntos de salida si estos recorridos cumplen con las llegadas estudiadas. En términos billarísticos, diremos que un billar "cuadra", cuando los ángulos del recorrido tienden a cerrarse, y que "alarga" en caso contrario. |
|
| Observemos dos casos prácticos en la figura 20.
Efectuaremos las pruebas usando solamente la bola 1. Colocamos ésta en la línea de salida 8 ataque 3, y jugamos con máximo efecto y golpe natural penetrado. Comprobamos que la línea prevista de llegada 5 - 7, no se ha cumplido, pues incidió sobre 6,5 en lugar de 7. Por tanto diremos que "alarga" en 0,5 rombo. Deberemos compensar esta diferencia restando 0,5 al punto de llegada, como este es 5, tenemos que: 5 - 0,5 = 4,5. Efectuando el cálculo, encontramos que: 4,5 = 8 - 3,5. Este será el resultado final del problema pues conocemos de antemano que alarga 0,5 rombo. Podemos decir, que este caso es una respuesta típica del billar con paño nuevo y recién estrenado. Vamos ahora a considerar que efectuamos la prueba en otra mesa de billar, con paño muy usado y expuesto a las corrientes de aire. Usaremos la misma figura 20 para demostrar este ejemplo. Supongamos que salimos de 5 y atacamos en 2, para alcanzar la llegada 3 - 9. En esta ocasión tampoco se alcanza la llegada prevista, puesto que incide justamente a 0,5 rombo del rincón. Diremos que "cuadra" 0,5 rombo. Compensaremos esta diferencia sumando 0,5 al punto de llegada 3, por tanto: 3+0,5 = 3,5. Efectuando el cálculo encontramos que: 3,5 = 5-1,5. El punto de ataque será 1,5. |
 Figura 20 |
| Resumiendo, podemos enunciar que "si el rendimiento de un billar no se ajusta a la teoría, deberemos compensar en más o en menos, el punto de llegada". Los dos ejemplos estudiados pueden considerarse como casos extremos, pues en general los rendimientos de las mesas cumplen la teoría con bastante aproximación, sin embargo, el rendimiento no es lineal a lo largo de todo el billar, pues a ángulos abiertos tiende a alargar, y a ángulos cerrados tiende a cuadrar. Esta distorsión de la linealidad, deberá ser bien observada por el jugador y compensada debidamente. | |
| He pretendido con este pequeño libro, y contando por supuesto con la gran ayuda del Billar Monitor, difundir entre la gran familia de aficionados al billar, los conocimientos que sobre el particular nos ha legado nuestro gran maestro Roger Conti, mediante un método didáctico, que pudiera ser asimilado y a la vez practicado por el estudiante. Con la salvedad, de que se han trasladado las llegadas, de rombo a rombo, para que sean visualizadas con más comodidad por el jugador y proporcionen una mayor agilidad de resolución.
Finalmente, sólo me resta desear a los jóvenes jugadores que quieren alcanzar más altas metas, los mejores éxitos para el bien de nuestro deporte. |


